The current tutoring activity I’m doing is a redemption tour for me. My first attempt at tutoring was a mess. The victim was my daughter and I managed to alienate math material for her so much that she hates it to this day Sorry, baby, if you’re reading this. I’m very, very sorry 😊. . That’s heartbreaking because I achieved the opposite of what I wanted. She is in college now and cautiously and apprehensively approaching the material again (she did statistics last semester).
My current victim is my nephew, 9th grade. I try to be more patient, less pushy and mean. Big change: I let the student drive the session. It’s office hour style with questions coming from student homework. We’re doing it over videoconferencing because we don’t live close together. You can read about the setup here.
So far so good, he seems to not hate it yet.
I, on the other hand, kinda like it because I have to find new twists to explain some material and I get the excuse to read up on things I forgot long time ago. I’ll give an example for each.
In math the current topic we’re dealing with is parabola. The exercise in the homework gives you the graph of a parabola with a grid such that you can recognize some nice integer $(x, f(x))$ pairs like in the figure below.
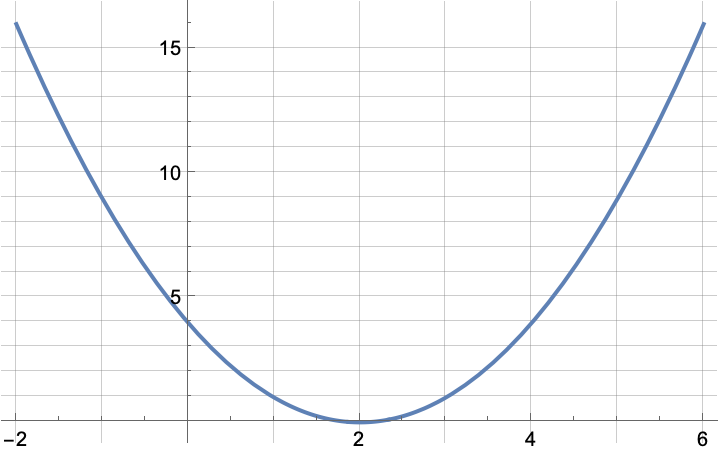
The exercise asks for the function equation given the graph. No problem, right? We just pick three pairs of $(x, f(x))$ from the graph, for example $(0, 4), (1, 1), (2, 0)$ and solve the system of linear equations coming from evaluating $f(x)= a x^2 + b x + c$ at those pairs.
Except they haven’t learned systems of linear equations yet. We need to figure out a different way to come up with the function equation. The exercise had some additional information: the parabola is not compressed or stretched. Meaning, it is identical in its form to $f(x)=x^2$, only shifted, in this case shifted to the right. The shifted function $f_s$ is identical in form to the original function $f(x)=x^2$, only shifted to the right along the $x$ axis. To compute a value $f_s(x)$ we have to find the corresponding $x’$ value according to the parabola form and evaluate $f(x’)$. The easiest identifying point is the vertex of the parabola. How much do you have to shift $x$ corresponding to the vertex of $f_s$ left to get to the vertex of $f$. From the graph it is visible that we have to shift two units left (shifting left means subtracting), so $f_s(x) = f(x-2)$. Of course we can do this algebraically also. We need to shift $x$ back by an unknown amount, say $a$: $f_s(x) = f(x-a)$ and the most convenient $x$ to use to solve for $a$ in this case is the $x$ corresponding to the vertex of $f$: $x = 2$.
$$ \begin{aligned} f_s(2) & = f(2-a) \\ 0 & = (2 - a)^2 \\ 0 & = 2 - a \\ a & = 2 \end{aligned} $$
So the function equation we need is $f_s(x) = (x - 2)^2$. What if the parabola (still not stretched or compressed, so identical to $x^2$) is shifted left by some amount, say $5$ (determined by looking where the vertex ended up? Similar reasoning leads to $f_s(x) = (x + 5)^2$. What if the parabola got shifted up by $3$? So instead of shifting along the $x$ axis it got pushed up along the $y$ axis, as in the figure below.
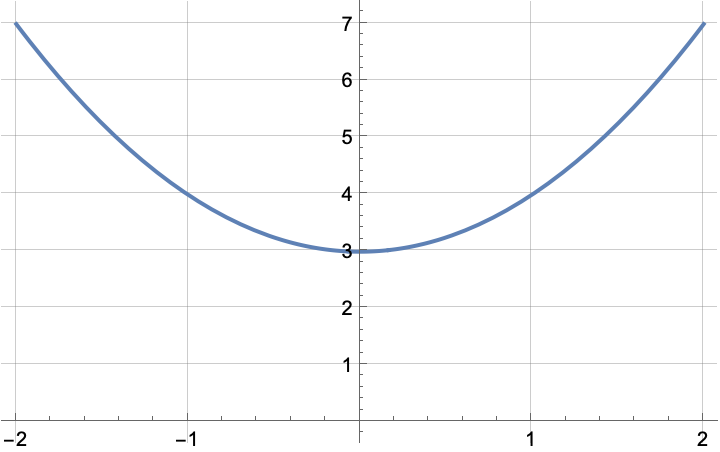
Well, the shifted value $f_s(x)$ at a given $x$ is pushed up by the constant amount $3$, so $f_s(x) = x^2 + 3$. You can combine the two shifts and get $f_s(x) = (x - 7)^2 + 3$ if it was shifted right by seven units and up by three. Etc, etc. The eye roll from the student or the reader at this point is magnificent 🙂. But solving a system of linear equations was not needed. One last thing before I move on to the second example of why I enjoy this tutoring activity. What if the parabola is compressed or stretched? Well, we can spy what the compressing/stretching factor should be. It is compressing the $x$ axis by pinching points together or stretching the $x$ axis by pulling them apart.
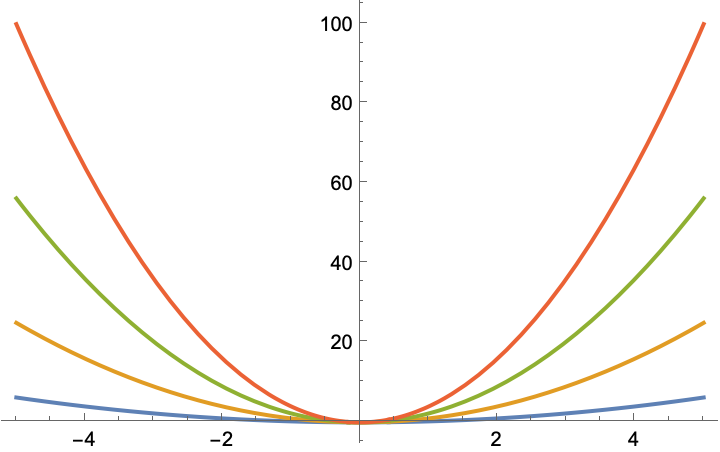
You can read from the graphs by how much you have to scale $x$ before feeding it into the original $x^2$ form. Or you can solve for the scaling factor algebraically. Combining that with the shifts covers all parabolas that have the opening facing up. If a parabola faces down instead, you invert the $y$ axis by computing it facing up and then multiplying the quadratic part by $-1$.
So obviously in general you are still dealing with three unknowns: $f(x) = (\alpha x - h)^2 + v$ where $\alpha$ is the compression factor, $h$ is the horizontal shift and $v$ is the vertical shift. But these are easier to read off the graph than the general form $f(x)= a x^2 + b x + c$. I know, 🙄. Respect, if you’re still here.
Ok, on to the second example, this one from physics. The topic is energy. What is energy? What are the different forms of energy? What are the units and how do they relate to those different energy forms. They are currently learning about kinetic energy, potential energy in a gravitational field of a large object (Earth), calorie burn energy and I think potential energy of a spring (I don’t remember). But how do you explain energy to somebody? It is quite abstract. What do all these energy forms have to do with each other and why is there conservation of energy? Hard questions.
Well, the best physics teacher in the world, Richard Feynman, is here to help: https://www.feynmanlectures.caltech.edu/I_04.html
Imagine a child, perhaps “Dennis the Menace,” who has blocks which are absolutely indestructible, and cannot be divided into pieces. Each is the same as the other. Let us suppose that he has 28 blocks. His mother puts him with his 28 blocks into a room at the beginning of the day. At the end of the day, being curious, she counts the blocks very carefully, and discovers a phenomenal law—no matter what he does with the blocks, there are always 28 remaining! This continues for a number of days, until one day there are only 27 blocks, but a little investigating shows that there is one under the rug—she must look everywhere to be sure that the number of blocks has not changed. One day, however, the number appears to change—there are only 26 blocks. Careful investigation indicates that the window was open, and upon looking outside, the other two blocks are found…
Read the whole thing, it is great. Anyways, without tutoring I wouldn’t have sought this gem and read it.