Majority

This Haskell cicada is another small problem from long time ago.

Given a set of marbles of different colors, find the majority color knowing it exists.

Let $M$ be the set of marbles and $|M| = n$. We know that there is a color $c$ such that

$$ |\{ m \in M: color(m) = c \}| > \frac{n}{2} $$

We prove the following lemma:

Given $x, y \in M$ with $color(x) \neq color(y)$, then the majority color in $M$ is also the majority color in $M \setminus \{x, y\}$.

Proof:

Let $c_0$ be the majority color in $M$ and let’s say $k > \frac{n}{2}$ marbles have it. We have two cases to consider:

• Case 1:

$$ color(x) \neq c_0, \text{ } color(y) \neq c_0 $$

Then $c_0$ appears $k > \frac{n}{2} > \frac{n - 2}{2}$ times in $M \setminus \{x, y\}$ too, so it is the majority color in the smaller set too.

• Case 2:

$$ color(x) = c_0 $$

Then $c_0$ appears $k - 1 > \frac{n}{2} - 1 = \frac{n - 2}{2}$ times, so $c_0$ is still the majority in the smaller set.

This concludes the proof of the lemma. $\Box$

Armed with the lemma we can do a recursive solution. We partition the set of marbles into two sets: marbles we haven’t processed yet and potential majority color candidates. Initially the unprocessed marble set is the original set and the potential candidates set is empty. We recursively shrink the unprocessed set of marbles using the lemma. We pair up one unprocessed marble with a potential majority candidate. If they differ, we know we can eliminate both. If their colors match we move the unprocessed marble into the set of potential majority candidates. The recursion ends when all the unprocessed marbles have been processed and the set of unprocessed marbles is empty. We know that a majority color exists so the set of potential majority candidates must contain only marbles with the majority color.

In the listing below the first parameter to the majority function is the list of unprocessed marbles (initially equal to the original set of marbles) and the second parameter is the list of potential majority candidates (initially empty).

{-# OPTIONS_GHC -Wno-incomplete-patterns #-}
module Majority (majority) where

majority :: Eq a => [a] -> [a] -> a
majority [] (y:_) = y
majority (x:xs) [] = majority xs [x]
majority (x:xs) (y:ys) = 
    if x == y 
    then majority xs (x:y:ys) 
    else majority xs ys

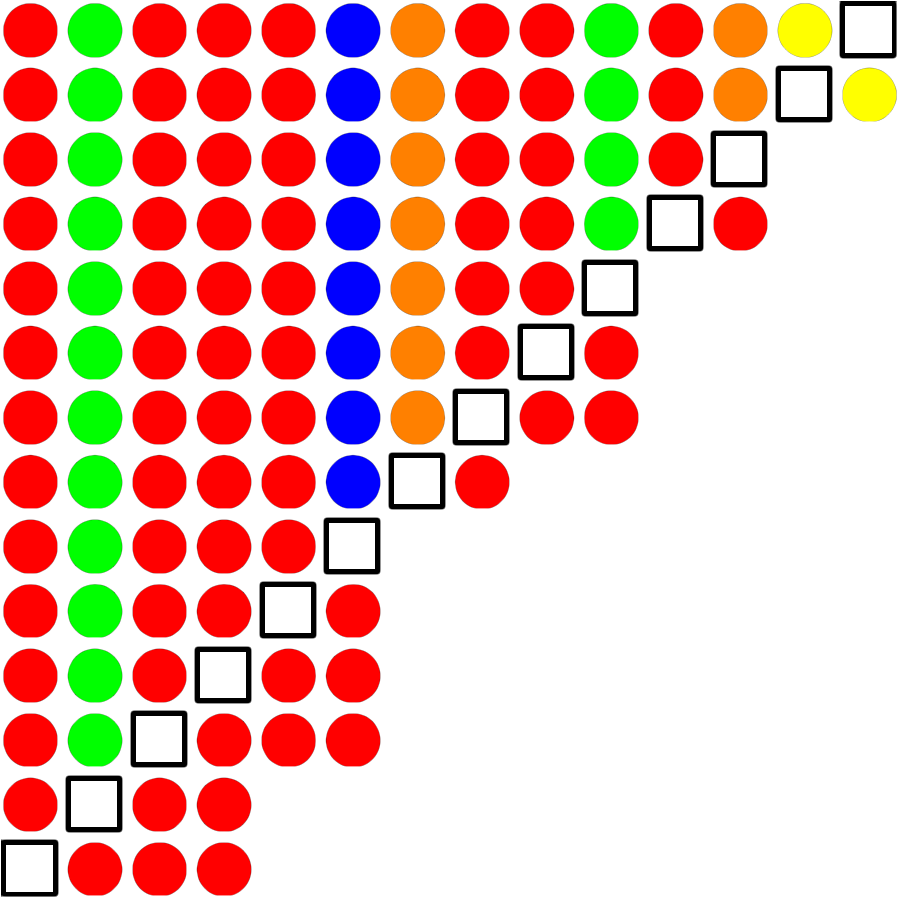
The figure below illustrates the algorithm with an example set of marbles. Each row in the grid shows the state of the two lists (unprocessed list and candidates list) after one recursive call. The two lists are separated by the white square. On the left of the white square is the unprocessed list and on the right are the majority candidates. Initially the original list is on the left of the square and nothing on the right. As the recursion proceeds, the marbles on the left either get eliminated together with their paired up candidate on the right (in case of color mismatch) or they move to the right (in case the colors in the pair match). The list on the left has its head next to the white square and goes from right to left, the list on the right also has its head next to the square and goes from left to right. Pairs are made from the two marbles on the left and right of the white square.