Imagine a 6 by 6 grid of squares, that can either be black or white.
It has to fulfill the following properties:
1. Each row and column needs to have 3 white and 3 black squares.
2. All black squares have to be orthogonally connected.
Prove that such a grid cannot exist.
- part 1: naive brute force exhaustive search
- part 2: smarter exhaustive search
- part 3: inductive graphs
- part 4: connected magic squares
- part 5: experiments
Note: in our digital representation black squares are ones and white squares are zeros.
This is part 5 of a series of posts about a puzzle I found on Mastodon and which I don’t yet know how to solve. In part 1 we decided to employ a brute force exhaustive search for solutions. In part 2 we improved the performance of the brute force search so it can handle magic squares of size six by six. In part 3 we tackled graph algorithms in a functional programming setting. In part 4 we converted our matrix into a graph and augmented filtering to reject graphs that are not connected.
In this part we run our code and stare at grids of examples. We use Mathematica to plot them. We have a convenience function in Mathematica that converts the Haskell list output to a Mathematica list:
toMMA[s_String] :=
ToExpression[StringReplace[s, {"[" -> "{", "]" -> "}"}]
This way we can output our examples in a ghci session, copy it into Mathematica and plot it there:
ghci> take 50 (connectedSquares 6 4)
[[[0,0,1,1,1,1],[0,1,1,0,1,1],[1,1,0,0,1,1],[1,0,0,1,1,1],...]]]
We use this plotting function in Mathematica:
plotExamples[xs_] := GraphicsGrid[Partition[ArrayPlot[#, Mesh -> True] & /@ xs, 5]]
For the expression take 50 (connectedSquares 6 4) we get:

What surprised me is that there are no connected magic squares of size five by five with three ones. You have to bump it up to four ones.

So far I got no idea how to solve this puzzle. ¯\__(ツ)_/¯
Update (I had to wait a little longer for these following two):
Seven by seven with four exists:

And again to my surprise, eight by eight with four also exists:

Since this last one exists, we can subdivide each grid cell into four and again find a solution (ie, if a solution for $n$ exists, then also for $2n$). It is clear that $n \in \{2, 4, 6\}$ are special cases. So I still have no idea how to prove this 🤷♂️. Maybe this will turn out to be just a fun, little Haskell programming exercise 😀.
Update 2
I made myself a Main.hs and compiled the code with ghc (I previously was just using interactive sessions with ghci). It seems ghc-compiled code is significantly faster. It also turns out there are many eight by eight with four ones examples:

There is a nine by nine with five ones:

There also is ten by ten with five ones:

Can we push our luck and try twelve by twelve ? Well, I tried. I knew it would take a while, so I added a notification to the command line:
magicsquare 12 6; osascript -e 'tell application "Messages" to send "magicsquare 12 6 finished" to buddy "xxx-xxx-xxxx"'
I took my dog for a long walk. She was exhausted afterwards.

No message from magicsquare. I made myself lunch. Still nothing. Kept waiting.

And then, many, many hours later

Still nothing. Let’s look why it is taking so long. A somewhat rough approximation of the search space being searched for a $n \times n$ case with $n$ even is:
$$ \binom{n}{\frac{n}{2}}^{n^2} $$
Using Mathematica we can calculate it for $n = 12$:
In[2]:= Binomial[12, 6]^12
Out[2]= 387314409522870177464536579782475776
It’s a very big number. Not as bad as the naive approach from part 1. There it would have been
In[3]:= 2^144
Out[3]= 22300745198530623141535718272648361505980416
But still way longer than the ten by ten case for example:
In[5]:= Binomial[10, 5]^10
Out[5]= 1032774265740240721281024
The exhaustive search strategy I implemented is not fast enough to cover such a big number of cases. But it gave me time to think. Here is a cool observation. For $n$ even, if you have a connected magic square of size $n \times n$ with $\frac{n}{2}$ ones where the connected component touches two opposite corners (or even weaker, touches two opposite corner side sections up to $\frac{n}{2}$ in length), then we can find a solution for $n + 2 \times n + 2$ with $\frac{n}{2} + 1$ ones by bracketing the opposite sides with right-angle brackets of ones of size $\frac{n}{2} + 1$. The figure below illustrates this:
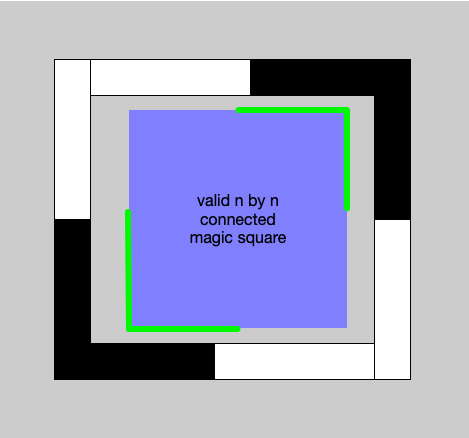
Assume the inner blue square is a valid $n \times n$ connected magic square with $\frac{n}{2}$ ones, where the connected component touches both green side brackets of the square. The green side brackets have side length $\frac{n}{2}$. We can then frame this blue square with the pictured frame where the black regions are ones. The frame is one cell thick and has side length $n + 2$. It’s easy to observe that both the connectedness and the magic property are preserved. The frame only adds a single one to each row and column of the new square. And because the outside ones touch the green region, we are still connected.
The ten by ten example above satisfies the requirements so we can use this observation to expand it to a twelve by twelve case:
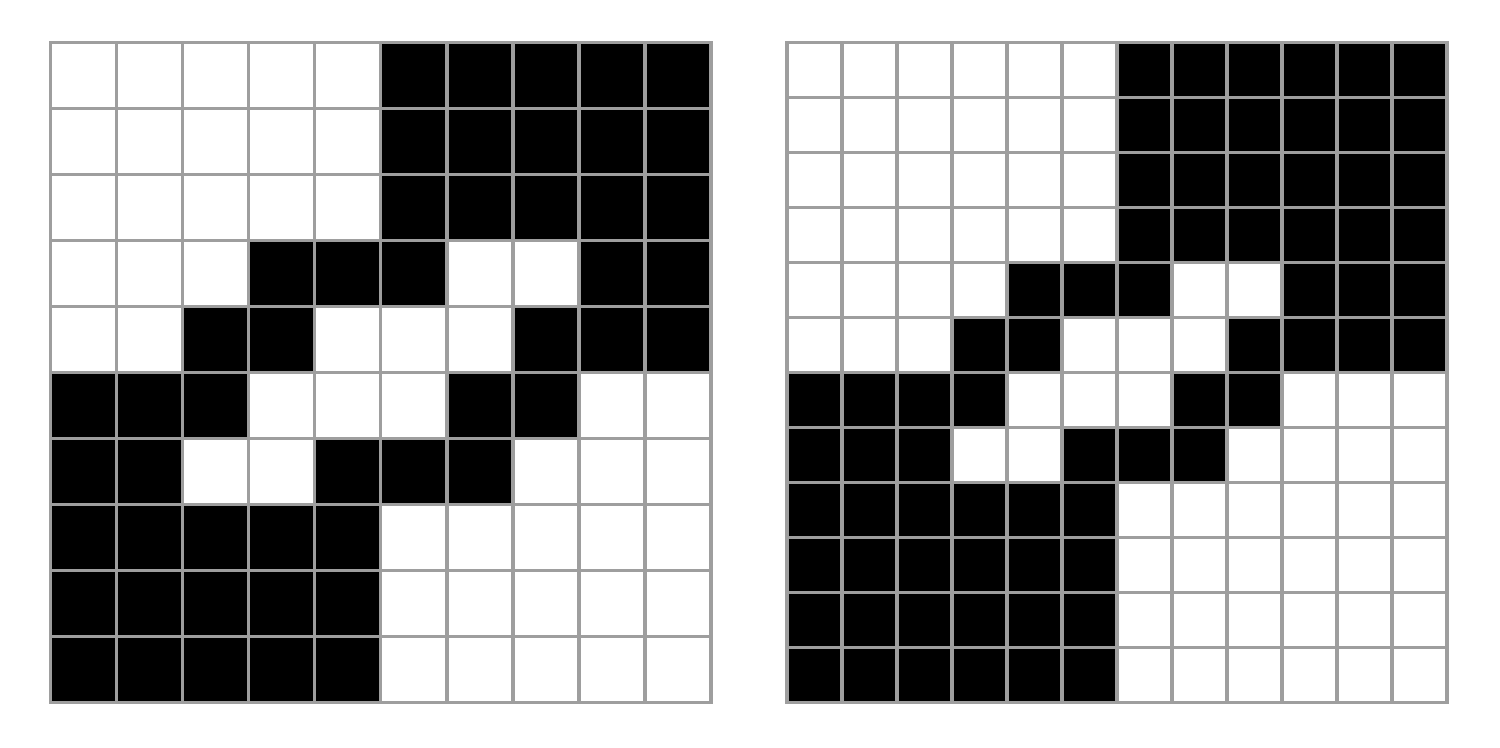
This covers the existence of such connected magic squares for all even numbers greater than six. We will end here. I feel like I pushed this puzzle far enough, can declare victory and move on 😀.
